Triangulation

Triangulation uses a single number and its positions in the puzzle to find other spaces in which that number belongs. Two instances of the number may determine the position of a third instance, hence: triangulation. However, triangulation works with with as few as one number or as many as four or five but triangulation seems like a good name so I'll stick with it.

Triangulation works by imaging that the rows or columns with a number are shaded. Here is our puzzle with rows and columns containing 2 shaded:

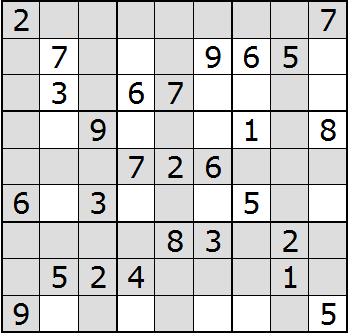
Because each block may only contain a single 2, we'll shade all the spaces in each block with a 2:

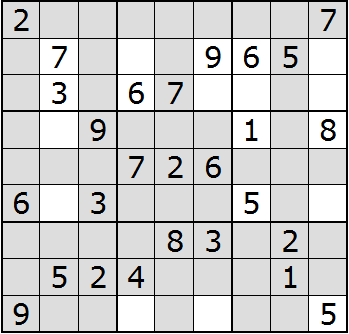
Each unshaded space without a number is a potential location for the number 2. Remember the goal, numbers 1 to 9 in each block, row, and column. Looking at the blocks from left to right, top to bottom, the second, fourth, and eighth blocks have two empty spaces. Block three has three empty spaces. There is a single unshaded space in block six. We can put a 2 there.

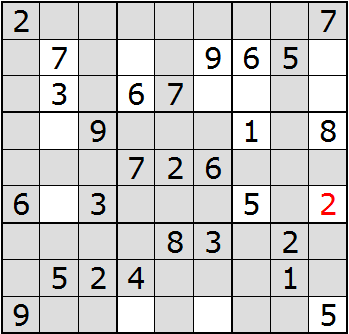
If you can imagine all that shading, go for it. But if you're like me, you can't so work with a single row or column of blocks. In the first column of blocks, the second and third columns contain 3. That leaves two unshaded spaces in the bottom block:

But there is also a 3 in block eight. If that row is shaded, there is a single, unshaded space in block seven. A 3 belongs there—Triangulation: the position of three 3s determines the location of a fourth 3:

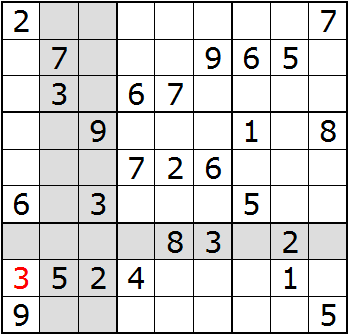
I'm only going to shade rows or columns, not the blocks, in the examples that follow just as I did in the example above.

Going through the puzzle one number at a time, we find:

  • 1: not enough information to place any 1s;
  • 2: 2 in block six(Click here to see the shading.);
  • 3: 3 in block seven (See above.);
  • 4: not enough information to place any 4s;
  • 5: 5 in the upper, left space of block eight (Click here to see the shading.);
  • 6: 6 in the middle space of the top row of block six (Click here to see the shading.);
  • 7: First, we place a 7 in the upper, left space of block four based two shaded rows:

With that seven in place and the 2 we placed earlier, we can put a 7 in the middle space of the bottom row of block six:

  • 8: Here's where ghost numbers come into play. We'll shade the first row of the bottom row of blocks—there is an 8 in it. We know from earlier that a 3 takes up a space in block seven so there must be an 8 in either of the two empty spaces in the bottom row of this block:

We can shade that row because we know there must be an 8 in one of those cells. With the last column shaded, we can put an 8 in the left space of the middle row of block nine:

  • 9: 9 in middle space of the top row in block one (Click here to see the shading.).

We are able to fill in eight spaces. If we do it all over again, we can fill seven more spaces:

    
 

 

The puzzle so far:
  • 1: still not enough information to place 1s;
  • 2: four 2s so we know the locations of all the 2s in the puzzle (Click here to see the shading.);
  • 3: not enough information to place 3s;
  • 4: not enough information to place 4s;
  • 5: not enough information to place 5s;
  • 6: one 6 (Click here to see the shading.);
  • 7: not enough information to place 7s;
  • 8: not enough information to place 8s; and
  • 9: we can place two 9s (Click here to see the shading.).

You may be able to solve easy suduko puzzles with just triangulation. In more difficult puzzles, after two rounds of triangulation, I use the elimination tool. As we're able to fill spaces with the elimination tool, we'll return to triangulation.

  

 

After two rounds of triangulation: